Dans la première partie de cette série, nous avons décortiqué le fonctionnement d’un procédé de chiffrement qui consiste à rendre secrète une information afin de pouvoir la transmettre à un destinataire sans être comprise par une personne étrangère à la conversation.
A l’issue de cette présentation, nous étions confrontés au problème suivant : comment passer à l’échelle lorsque de nombreux groupes d’utilisateurs différents souhaitent communiquer entre eux des données de manière sécurisée ?
2 Utilisation du chiffrement asymétrique :
C’est là que le chiffrement asymétrique va permettre de simplifier les choses.
Dans ce système, chaque utilisateur dispose d’un couple de clés liées entre elles, qui lui sont personnelles, qui seront utilisées pour chiffrer et déchiffrer les messages.
2.1 Principe
Ce procédé doit répondre à certaines contraintes :
- Il doit être impossible de déduire l’autre clé du couple si l’on en possède une,
- La première clé doit permettre de déchiffrer un message signé avec la deuxième, et inversement.
Dans la pratique, l’une des deux clés est gardée secrète (on dit aussi « privée ») et l’autre est rendue publique. Chaque utilisateur dispose donc de sa propre clé secrète et tout le monde peut disposer de la clé publique, ce qui élimine le problème de l’échange de clés.
Plus précisément : Alice dispose d’une clé publique KApb et d’une clé privée KApk, Bob d’une clé publique KBpb et d’une clé privée KBpk. Pour envoyer un message à Bob, Alice va chiffrer le message avec la clé KBpb que tout le monde connaît, puisqu’elle est publique ; mais seul Bob sera en mesure de le déchiffrer puisqu’il dispose de la clé secrète associée à sa clé publique. Si Eve veut envoyer un message à Alice et à Bob, alors elle peut chiffrer le message avec KApb et KBpb, sans avoir besoin de renégocier de clés avec ces utilisateurs.
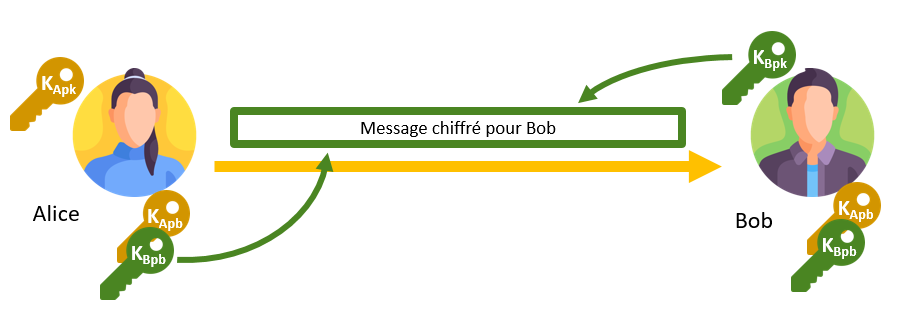
Avec cette méthode, chaque utilisateur doit disposer des clés publiques des autres utilisateurs, et de sa propre clé privée :

Ce partage de clés entre tous les utilisateurs est aisé à réaliser de manière automatisée et transparente en entreprise, où les ordinateurs professionnels des utilisateurs disposeront de l’ensemble des clés des autres utilisateurs, et pourront les mettre à jour automatiquement de manière centralisée lors de l’ajout ou la suppression d’un collaborateur. On parlera alors d’infrastructure de clés publiques, ou PKI (Public Key Infrastructure).
Pour Internet, c’est plus complexe, puisqu’il n’est pas possible pour chaque ordinateur de disposer des milliards de clés de toutes les autres personnes ou sites disponibles. Le mécanisme de certificat entre alors en jeu.
2.2 Certificat
Dans cette partie, nous nous plaçons dans le cas concret d’une navigation sur Internet : Alice consulte plusieurs sites différents, et attend évidemment que l’ensemble de ses communications avec ces différents sites soit chiffré.
Comme nous l’avons vu précédemment, l’ordinateur (dans ce cas précis, le navigateur Internet) d’Alice ne peut pas posséder l’ensemble des clés publiques de tous les sites possibles : une telle infrastructure serait extrêmement difficile à maintenir et bien trop gourmande en ressources. En pratique, les navigateurs ne contiennent que quelques certificats, que l’on assimilera à des clés publiques pour l’instant, de quelques émetteurs de certificats.
Ces informations sont disponibles dans tous les navigateurs, par exemple sous Firefox en allant dans « Paramètres > Vie privée et Sécurité > Certificats > Afficher les certificats »
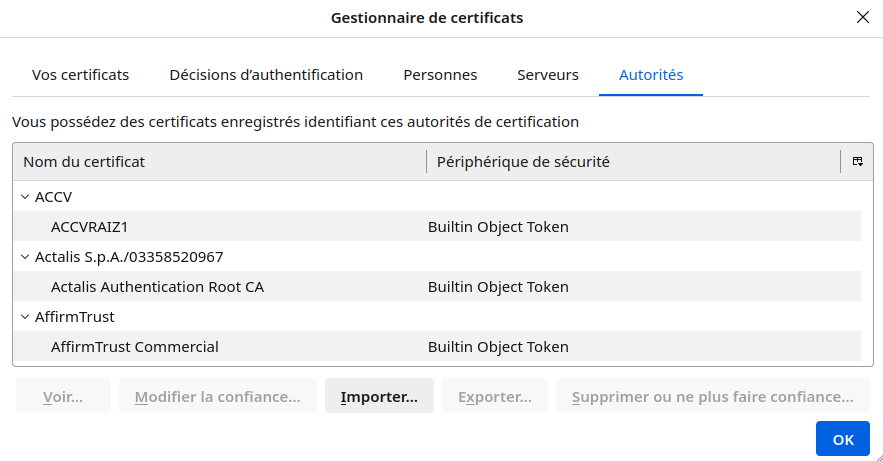
Dans la section « Autorités » sont répertoriés les certificats racines d’autorité (CA ou AC) qui font foi pour l’ensemble du web (ils peuvent être différents selon le logiciel utilisé ou son niveau de mise à jour).
Ces « clés publiques » sont donc connues « en dur » dans les navigateurs, et sont considérées « de confiance ».
Pour être considéré « de confiance », un site web sur Internet va devoir présenter un certificat signé par l’une des autorités de certification. Ce mécanisme de signature sera traité en détails dans le chapitre suivant.
Prenons l’exemple de Wikipédia :
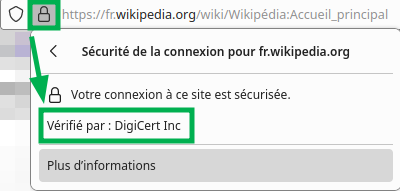
En cliquant sur le « cadenas » présent avant l’URL dans notre navigateur, nous obtenons l’information que la connexion est sécurisée, et que le certificat est vérifié par « DigiCert Inc », que l’on peut effectivement retrouver dans la base des certificats d’autorité (CA) de notre navigateur.
Cliquons sur « Plus d’informations », puis sur « Afficher le certificat » :
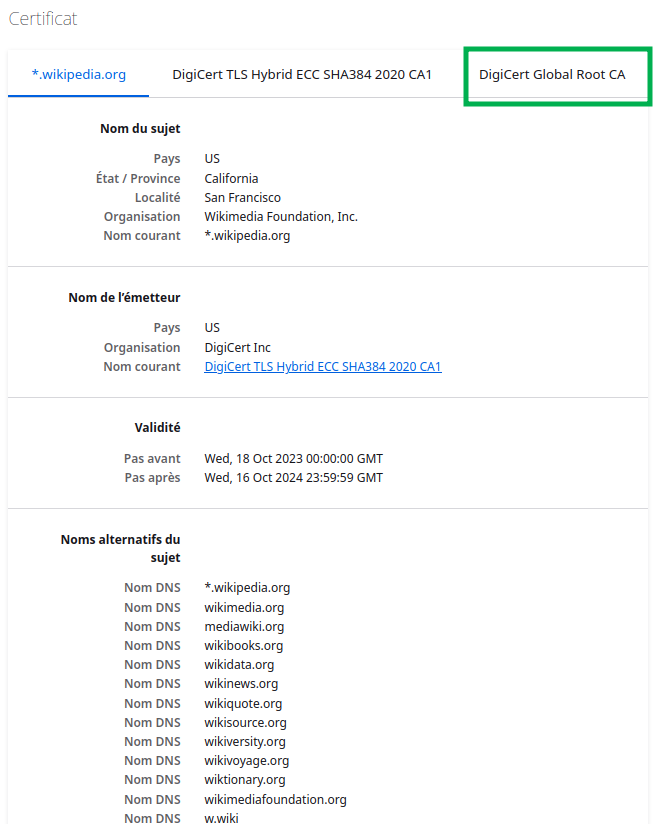
Le premier certificat visible est celui présenté par le site web consulté, ici wikipedia.org. Nous obtenons plusieurs informations : il est valide jusqu’en octobre 2024, pour un ensemble de noms DNS variés : par exemple les domaines wikipedia.org, wikidata.org, wikiquote.org, etc, ainsi que d’autres informations techniques.
Deux autres certificats sont présents dans la fiche :
« DigiCert TLS Hybrid ECC SHA384 2020 CA1 » et « DigiCert Global Root CA ». Il s’agit de la « chaîne de certificats » : chacun est signé par le précédent, le certificat au bout de la chaîne faisant partie de la base de confiance de notre navigateur. C’est précisément ce point qui est vérifié lorsque le fameux « cadenas de sécurité » est affiché à côté d’une URL. Cela signifie simplement que le site web que nous consultons dispose d’un certificat généré par une des autorités de confiance.
Note :
Aujourd’hui, il est extrêmement simple, parfois gratuit, de disposer d’un tel certificat pour son propre site web, par exemple avec Let’sEncrypt. La présence d’un « cadenas » à côté d’une URL n’est donc pas suffisante pour se considérer « en sécurité » sur un site.
Analysons les informations présentes un peu plus bas dans le détail du certificat :
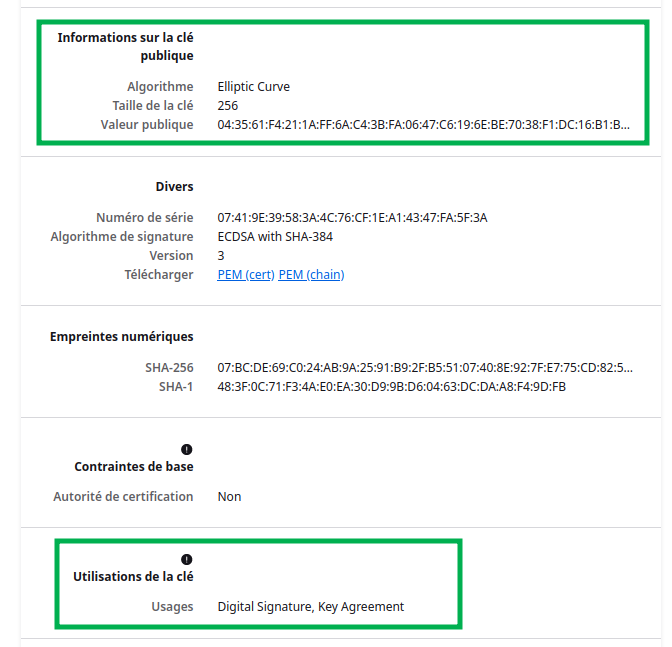
Là encore, de nombreuses informations sont présentes. Retenons celles encadrées en vert : le certificat dispose d’une clé publique basée sur un algorithme de courbes elliptiques d’une taille de 256 bits et commençant par « 04:35:61… ».
Lorsque Alice va se rendre sur Wikipedia, son navigateur va opérer automatiquement quelques étapes.
Il va d’abord consulter le certificat du site, vérifier qu’il est valide et signé par une autorité de certification reconnue, puis utiliser la clé publique fournie dans le certificat pour valider les premiers messages émis par le site et initier une communication sécurisée avec ce site. Il s’agit d’un handshake TLS, ou poignée de main, en français.
Nous résumons ci-dessous un handshake TLS pour les premières versions de TLS.
Voir plus d’informations dans l’article de CloudFlare.
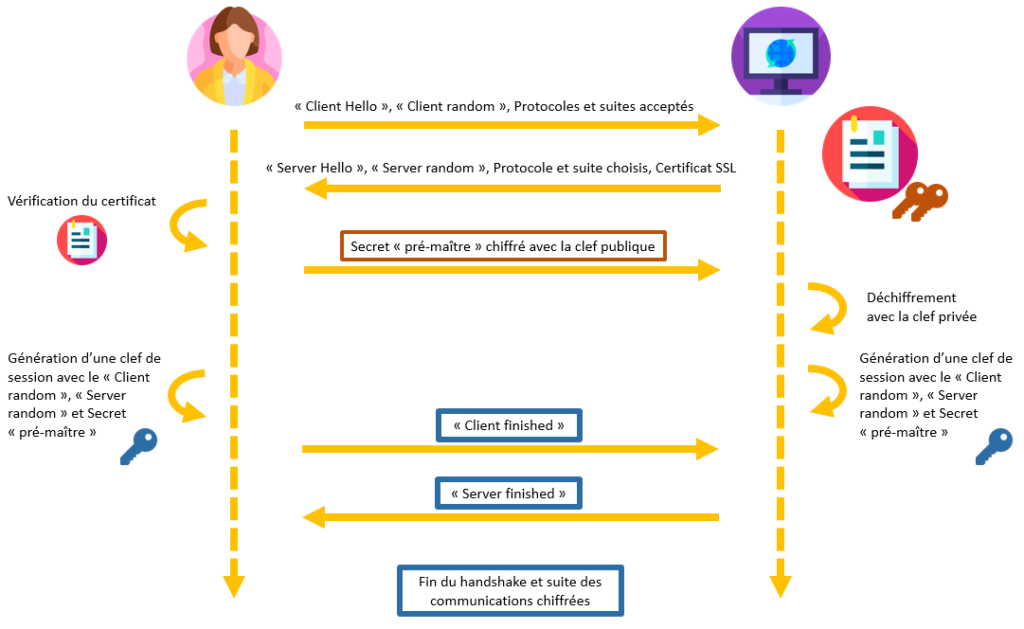
- Dans le premier message du schéma ci-dessus, Alice (ou plutôt son navigateur) initie la connexion et informe le serveur des protocoles et algorithmes dont elle dispose.
- Le serveur répond avec un protocole et un algorithme de son choix parmi ceux proposés par Alice, et fournit son certificat.
- Alice vérifie le certificat de son côté, puis envoie un « secret » chiffré avec la clé publique obtenue via le certificat. Chacun de son côté génère alors une clé de session, et vérifie que tout s’est déroulé comme prévu en échangeant un message chiffré avec cette clé. Ils doivent être en mesure de déchiffrer le message « finished » de l’autre.
- La clé de session en bleu dans le schéma est une clé symétrique qui sera utilisée pour l’ensemble de la session TLS et permet des performances plus rapides que le chiffrement asymétrique, utilisé lors de la transmission de cette clé de session.
Nous avons donc vu en pratique comment fonctionne le mécanisme de chiffrement asymétrique utilisé pour la plupart des communications sur Internet grâce aux mécanismes de certificat. Dans l’exemple présenté plus haut, seul le client vérifie l’identité du serveur, mais il est également possible au serveur de demander une vérification de l’identité du client au travers de son propre certificat. Il faudra alors que le certificat du client soit signé par une autorité reconnue par le serveur, généralement lui-même.
Voyons à présent plus en détails le mécanisme de signature.
2.3 Signature
Nous avons expliqué qu’un client pouvait « vérifier » un message à l’aide d’une signature électronique. Le procédé de signature peut être représenté comme l’inverse de celui du chiffrement asymétrique : l’utilisateur va se servir de sa clé privée pour chiffrer une partie d’un message, que le destinataire pourra déchiffrer à l’aide de la clé publique dont il dispose. Si la partie du message correspond bien à ce qui est attendu, alors le destinataire aura la preuve que l’utilisateur est bien celui qu’il prétend être, puisqu’il est le seul à détenir la clé privée.
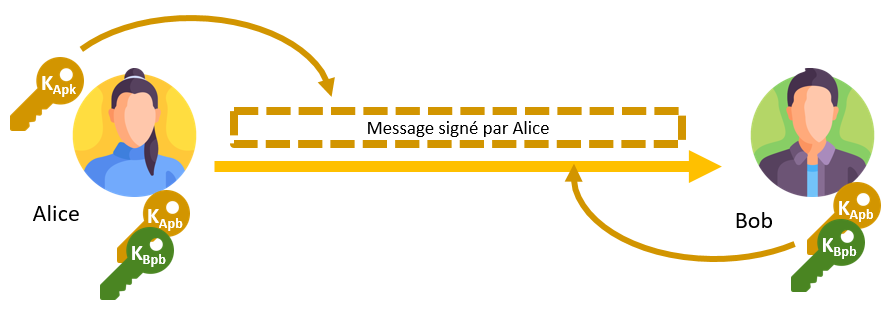
En pratique, cette « partie » de message correspond à une empreinte cryptographique, ou hash, dont le processus mathématique sera détaillé dans le prochain article. Pour l’instant, considérons que cette « partie » du message est le message lui-même.
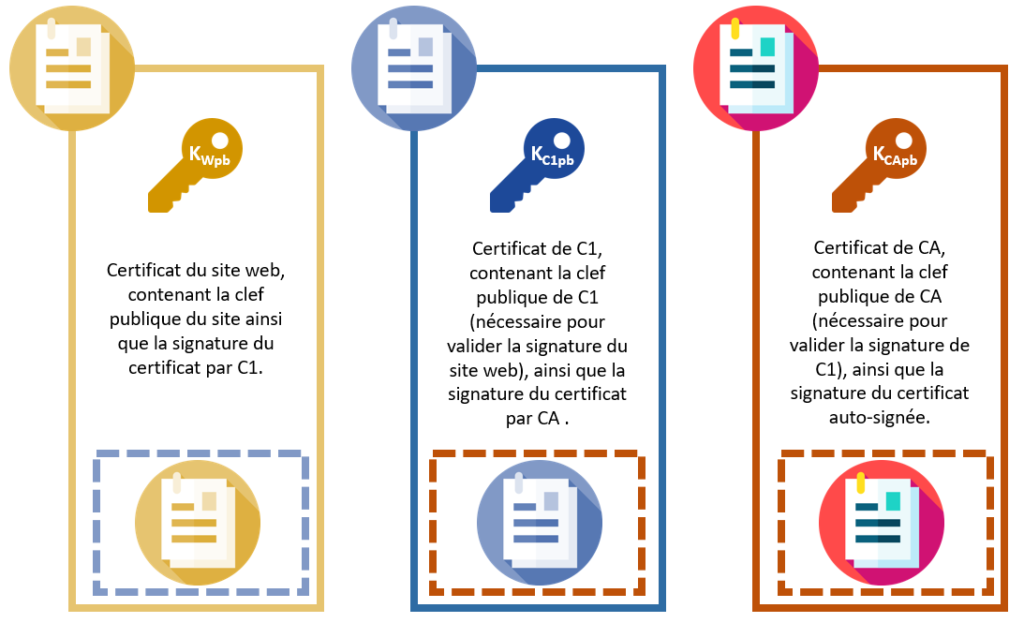
Reprenons l’exemple fourni en Figure 9 pour illustrer le processus de vérification d’un certificat.
Le certificat de Wikipédia est signé par une entité CA1, cela signifie que le certificat de Wikipédia (en jaune ci-dessous) est concaténé à une copie de ce même certificat, mais signée, c’est-à-dire chiffrée avec la clé privée de CA1 (le chiffrement avec une clé privée est représenté en pointillé).
Pour valider cette signature, l’utilisatrice Alice doit récupérer le certificat de CA1 (en bleu), qui contient la clé publique KC1pb. Mais Alice va vouloir, là aussi, vérifier l’authenticité de ce certificat, elle va donc consulter la signature de CA1, cette fois chiffrée avec la clé publique de CA (en rouge), qui est une autorité de certification reconnue, à laquelle Alice (ou du moins son navigateur) fait confiance.
Alice utilise donc KCApb pour « déchiffrer » la signature présentée par CA1. Si celle-ci correspond bien au certificat, alors Alice saura, avec une absolue certitude, que c’est bien CA qui a délivré ce certificat à CA1, puisque seul CA possède la clé privée associée qui a permis cette signature.
Alice accorde désormais sa confiance à CA1.
Elle peut donc utiliser la clé KC1pbpour vérifier la signature présentée par Wikipédia. Si elle retrouve bien le certificat après « déchiffrement », alors elle saura que c’est effectivement CA1 qui a émis cette signature, puisqu’il est le seul à détenir la clé privée associée. Après ce deuxième rebond, Alice fait désormais confiance à Wikipédia, et peut utiliser KWpbpour initier un handshake TLS.
Imaginons maintenant le cas d’une entreprise, comme présenté en Figure 6, où chaque utilisateur dispose de sa propre clé privée et de l’ensemble des clés publiques des autres collaborateurs, grâce à la PKI. Dans cette entreprise, Alice souhaite envoyer un message sécurisé à Bob. Si elle ne le signe pas, alors Charlie, en se plaçant au milieu de la communication (attaque Man-in-the-Middle), pourrait modifier le message, puisqu’il connaît lui aussi la clé publique de Bob.
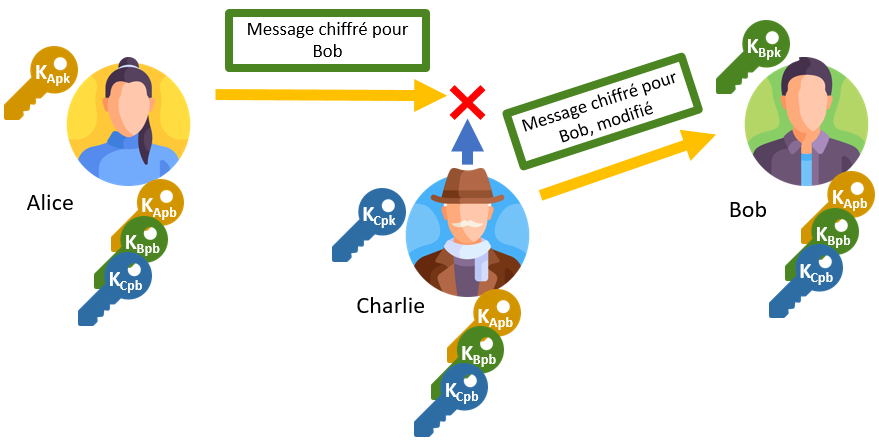
Dans cet exemple, il est important de comprendre que Charlie ne peut pas lire le message envoyé par Alice, puisqu’il est chiffré avec la clé publique de Bob. Cependant, dans sa position, il peut tout à fait émettre un autre message, sans que Bob ne puisse déceler le subterfuge.
Le mécanisme supplémentaire de signature permet à Bob de s’assurer que l’émettrice est bien Alice, et que le message n’a pas été modifié :
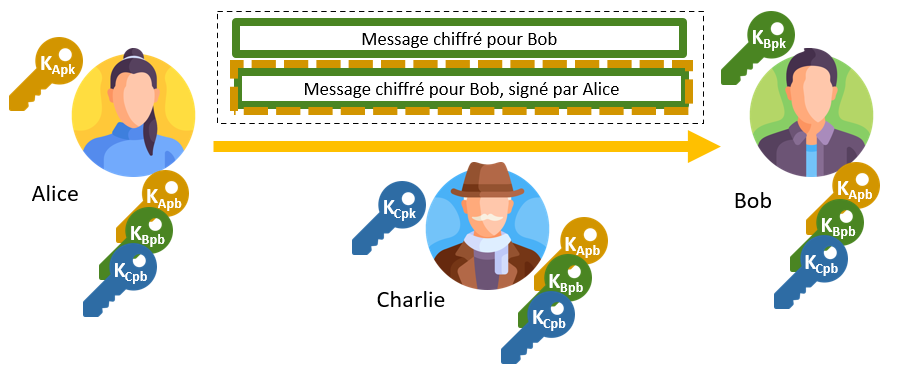
Cette fois, Alice envoie toujours son message chiffré avec la clé publique de Bob, le rectangle vert, mais elle ajoute une copie de ce message chiffré signée, c’est-à-dire chiffrée avec sa clé privée.
Lorsque Bob va utiliser la clé publique d’Alice pour déchiffrer la signature, s’il retrouve bien le même message, alors il sera sûr que c’est bien Alice qui l’a émis. Ce procédé permet la non-répudiation : il prouve qu’Alice a bien émis le message, et la vérification de l’intégrité du message : en comparant les deux éléments, Bob s’assure que rien n’a été modifié dans la transmission.
Ici, Charlie ne possédant ni KApk ni KBpk, il ne peut pas déchiffrer le message pour Bob, et ne peut pas le modifier puisqu’il lui faudrait également modifier la signature.
Dans un environnement d’entreprise de type Active Directory, toutes ces opérations de chiffrement et signature sont automatisées et complètement transparentes pour les utilisateurs.
Dans nos exemples, il est systématiquement nécessaire d’envoyer une copie totale du message pour pouvoir le signer, ce qui double les besoins en bande passante. En pratique, une signature consiste à chiffrer avec sa clé privée seulement une partie d’un message, que l’on appelle l’empreinte et qui est le résultat d’une fonction de hachage.
2.4 Conclusion
Dans cette partie nous avons vu le fonctionnement du chiffrement asymétrique, qui permet d’éviter d’avoir à échanger une clé initiale avec un destinataire. Nous avons également vu en détails le mécanisme de signature, notamment appliqué aux certificats, qui simplifie la distribution de clés publiques sur Internet et permet d’assurer l’authenticité d’un message.
Dans la dernière partie de cette série, nous décrirons le fonctionnement des fonctions de hachage et leur application pour le contrôle d’intégrité et la sécurité du stockage des mots de passe.
Article rédigé par : Florence H. , consultante chez Coralium
Si vous voulez en savoir davantage sur nos offres, en lien avec le sujet de l’article, nous vous proposons de découvrir : Politique de Sécurité des Systèmes d’Information (PSSI)
Références :
L’ensemble des icônes utilisés dans les schémas proviennent de Freepik sur Flaticon
